数値解析の専門家で、応用数学について研究している奥村真善美講師にお話を伺いました。

About Me ( OKUMURA Makoto )

元々は高校の数学の先生を目指し、京都教育大学に進学したのですが、大学数学の奥深さに触れ、高校までで触れてきた数学は氷山の一角に過ぎないことを知り、より深く数学を学びたいと強く感じるようになりました。また、ゼミ活動では非常に充実した時間を過ごせ、このまま就職するのではもったいないと感じ、大学院進学を決めました。また、情報の教員免許取得のため受講していた授業でプログラミングに触れていたことに加え、指導教員の紹介もあり、大阪大学大学院情報科学研究科に進学しました。大学院では元々興味のあった、実際の現象などを表現するような微分方程式の数値計算についての研究に取り組み、修士号、博士号の学位を取得しました。微分方程式の数値計算は現在でも継続して取り組んでいる研究分野になります。

Research

人口の変化や、加熱・冷却による水温の変化など、身の回りの様々な現象・事象は、しばしば微分を用いた数式、微分方程式によって数学の問題として表現されることがあります。そして、そのような微分方程式を解き、その解を用いて、物理量や数量の変化の予測を行うことがあります。数年前、ニュースなどでよく見かけた新型ウイルスの感染者数の予測もその一つになります。

通常、予測には実験による検証が有効ですが、その実験が難しかったり、コスト面で何度も実験ができなかったりする場合、微分方程式が活躍します。ただ、より現実性を求めた微分方程式は複雑になることが多く、そのような数式はもはや手計算で解くことが困難となります。そこで数式をプログラムで解くという方法があり、それは数値計算・数値シミュレーションと呼ばれます。しかしながら、問題によっては汎用的な数値計算手法ではうまく計算できないことがあり、そのような問題に対し、何らかの優れた計算手法で数値計算する必要があるのですが、その一つに構造保存数値解法と呼ばれる手法があります。問題の物理的な背景（例えばエネルギー保存則などの物理法則）などを保った手法で、以下の利点があります。

• 安定的な計算が可能
• 数学的な解析（シミュレーションの誤差の見積もりなど）がしやすい

以下は、惑星の運動を表現する微分方程式を、汎用的な方法で計算した場合（左図）と有名な構造保存数値解法(Greenspan(1984))で計算した場合(右図)の結果です。

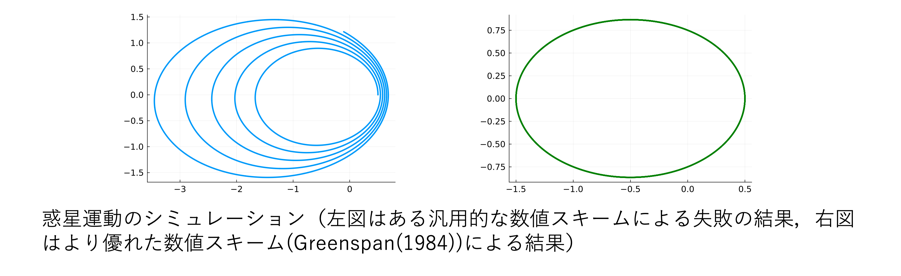
構造保存数値解法では、綺麗な楕円軌道が描けていますが、汎用的な数値計算方法では、段々とずれが大きくなっていることが見て取れます。計算方法の違いが実際の計算結果に大きな影響を及ぼすことに興味をもち、この構造保存数値計算に関する研究を精力的に行うようになりました。数値計算手法はこれまでに様々なものが提案されていますが、考える数式によっては、これが最善であるとまだ決まっていないこともあります。そのため、ひらめき・工夫次第で優れた成果を上げることが可能である点がこの分野の面白い点であると感じています。既存の手法よりも精度の良い手法を設計できたとき、考えた方法が実際にコンピュータ上で動き、良い結果が得られたときの達成感はひとしおで、それらの点にやりがいを感じます。また、微分方程式が対象とする範囲は幅広く、物理や生物、経済などへの応用や、数学、コンピュータといった分野を行き来し、多様なスタートラインで研究テーマを設定できる点が面白い点です。

KONAN’s Value

プレミア・プロジェクトをはじめとする、通常の授業や専門分野の垣根を超えた学びが、甲南大学ならではの特色であり、ステータスだと思います。また、学生・教員間の距離が近く、また優秀な先生方が揃っていることも学生にアピールしたい価値だと考えます。そして、甲南大学では、学会発表や資格取得のための支援制度が充実している点が大変魅力的だと感じています。仮に自分が学生に戻って、しかも知能情報学部の学生であったとしたら、「競技プログラミングチャレンジ」や「ディープラーニング入門」といったプロジェクトにチャレンジし、それと並行して正課の授業では、数学系、AI系の科目を重点的に受講したいです。そして、学会発表等の支援制度を生かして、積極的に学会にも参加したいです。これらの充実した環境こそが、甲南大学の大きな魅力だと考えます。

Private

Profile